Papal infallibility

The first post discussed the theory of STR and what the theory is trying to achieve.  There are 2 postulates or Einstein’s ‘laws’, which the science says are infallible and proven. 

The first postulate is that the laws of physics apply to all objects universally, as long as an ether or medium is not present.  ‘Laws of physics’ refers to the Catholic Galileo’s work in the 17th century and his law of inertia, summarised as: "Objects move with constant speed in a straight line when no external agent is acting on them”.

The second rule or postulate is that the speed of light or its velocity is constant for all objects regardless of their motion.  Again, this is similar to Galileo’s own experimental proofs. 

Einstein’s ex-cathedra postulate pronouncements are now deemed infallible and eternal.  These postulates surround and protect his STR theory.  The postulate and rules by themselves may well be sensible.  I don’t think they prove much of anything if we extend the postulates to the STR itself or the physical world.  Postulate one is basically unprovable.  Postulate 2 would not hold outside of a vacuum.  STR itself, in toto, is largely premised of course, on mathematics and in particular endless pages of dense equations. 

As Einstein supposedly remarked, not more than a dozen people on the planet would understand the theorem.  Maybe that was the whole point.  The layman with his curiosity and his weathered dirty hand on a shovel handle, may inquire as to what connection exists between the endless equations with their odd symbols, and the physical world.  He is answered with more maths and sometimes ridicule.

This post carries on from the introductory post, looking specifically at the mathematical foundations of the theory.

Galilean Transformation

By 1632 the Catholic Galileo had developed complicated equations which would be the basis of mechanical physics.  These equations described the transformation between the coordinates of two inertial frames (objects on a grid).  The equations are the basis of STR theory.  In essence Galileo’s transformation model can be summarised as: 

x¹  = vt -> where x is a coordinate of an event in one inertial frame (called S usually, with S being an object eg a moving train); x¹ is the coordinates of the same event in another inertial frame (S') moving at a constant velocity

y¹ = y  -> the same as x in the context of y

z¹ = z  -> same as x, y, in the context of z

t¹ = t where t = inertial time

In this theorem the transformations in the y and z directions are identity transformations, which means that there is no change along those axes.  The above is very similar to what is deployed in the STR.

Using the above maths Galileo describe the transformations between frames of reference at speeds much less than the speed of light.  It is not relativistic.  The theory cannot describe the relationship between space and time at relativistic speeds.  The Lorentz transformation theory by contrast, can articulate space and time at all relativistic speeds, including at the speed of light. 

STR maths & Lorentz

The Galilean transformation was superseded by the Dutchman Hendrik Lorentz’s equations or the ‘Lorentz transformations’, published in 1895.  It is undeniable that much of STR is derived from Lorentz though Einstein did not credit the Dutchman.  It is well-documented that Albert Einstein corresponded with Lorentz, and he had studied Lorentz's work.  The Lorentz transformations describe the mathematical relationship between the coordinates of events in different inertial frames and are the core of Einstein's theory of special relativity.

In their correspondence, Lorentz and Einstein discussed various aspects of electromagnetism, and Einstein was familiar with Lorentz's efforts to reconcile the phenomena of electromagnetism with the principles of classical Galilean mechanics.  Einstein took Lorentz’s work and extended it, adding the 2 postulates analysed in the first post, and E=mc2 or the conversion of energy and mass.  This would be proven in nuclear reactions.  E is the energy of the object, m its mass, and c is the speed of light in a vacuum. 

In reading both theorems I am not convinced that Einsteins’ theory is that much different.  Einstein uses Lorentz whole hog and adds E=mc2, a formulae developed by others though he stated he arrived at it independently.  I don’t find this convincing.  For the record, E=mc2 is initially an output of electro-magnetic theory, with Maxwell and others (for example, the British scientist J.J. Thomson, in 1881, and the Italian Olinto De Pretto, in 1903), being its true inventors, not Einstein.  Einstein dispensed with the ‘ether’ (luminiferous particles which interact with light and electro-magnetism, which is indeed different than the idea of ‘dark matter’ which does not interact with light).  He reformed the velocity of light to be a constant in a vacuum as well as proposing the exchange of energy with mass. Lorentz’s ideas are the real foundation of STR.

Lorentz’s theory

Lorentz’s calculations run to many pages.  In summary and to simplify some core aspects of the theory found in textbooks and on sites would be the following.

 

We can see the similarity with, and the use of Galileo’s transformation equations.

Lorentz’s theorem can be summarised in the following way:

1.     -t = time and x = space coordinates for one reference object, called S, moving at a certain velocity or v, relative to another reference object (or frame) called S¹

2.     v = the relative velocity between two inertial frames of reference or 2 objects within the same or different coordinates

3.     -For both objects S and S¹, coordinates or location maps covering both objects, are calculated using the variables, y, z an y¹, z¹ for both objects along the y and z axes

4.     -The z axis is a 3^rd dimension axis to imitate space is added to the above 2-dimensional diagram (the z axis was added in 1908, by Einstein’s math professor Hermann Minkowski)

5.     -c is the speed of light (for Einstein, this meant only a vacuum)

6.     The symbol γ is gamma or the Lorentz factor given below

 

The full equations and explanations can be found in any physics textbook online.  Many sites possess calculators where you can stroll through the theorem against a thought or paper experiment. 

The maths is difficult to wade through. 

A key difference between the 2 theorems is that Lorentz, like Maxwell and others, believed in an ether, or a medium in space which could interact with and propagate light, whereas Einstein did not.  However, both theories are so similar that they are conflated with each other, with STR categorised as the ‘Lorentz-Einstein model’.  Lorentz’s theory in and of itself is not relativistic, but Einstein’s is.  However, proofs offered for STR include the relativistic outputs of Lorentz’s equations.  This is both tautological and usually tangential.  You cannot use part of a theorem to prove the theory.

What does it mean?

The maths is abstract but can be applied to moving objects.  In his 1905 paper, Einstein used the analogy of a train and an observer on a train platform.  Assume we have an observer on a train platform, watching a train moving past the station at 60 mph.  Let’s put two objects emitting light, one at the beginning of the train, and one at the end of the train.  Calculations can be made to show the separation in time between when the lights flashed as seen by either the platform observer, or a second observer seated in the train in the middle of the car. 

Logically the person in the train would never see the flashing lights but that reality is dismissed in favour of trying to prove the relativistic nature of objects in motion and their light signals as seen by the 2 observers, one static on a platform, the other in a train moving at 60 mph away from the platform.  What does it mean?

1.     The Lorentz transformation purportedly shows that time and space are not absolute and can be different for observers in relative motion.

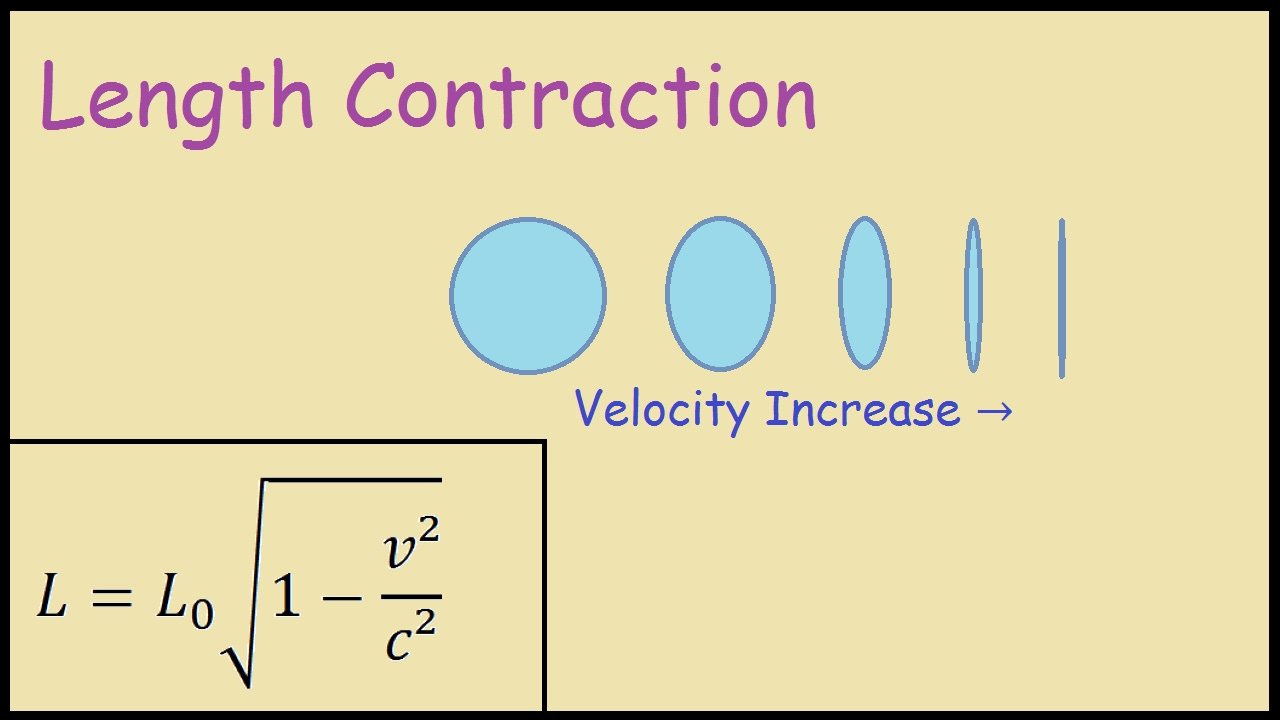
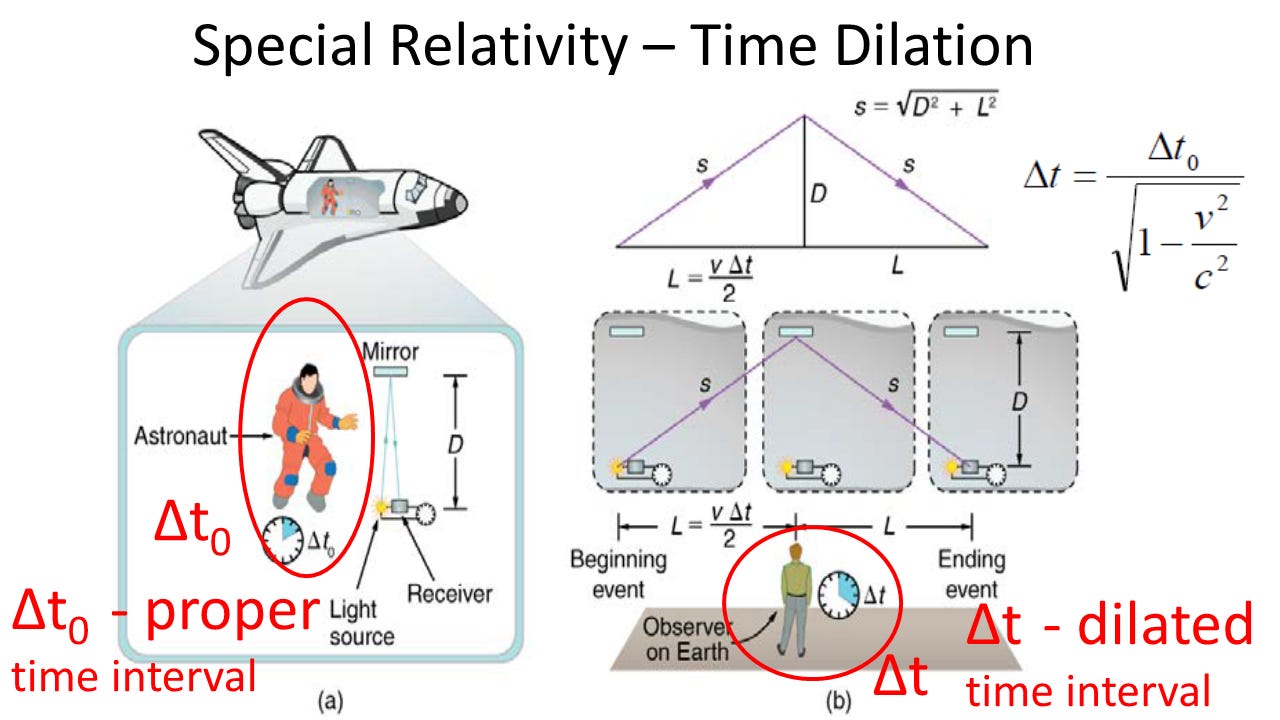
2.     The Lorentz factor accounts for the relativistic effects of time dilation and length contraction with the length (or mass) of an object becoming smaller as it moves away from an observer.  

Lorentz offers the ‘transformation’ equations to show relativity in space and time.  He also uses his ‘factor’ to ‘prove’ relativity between objects in time dilation (the twin’s paradox) and length contraction. 

Based on the above ideas, perhaps the key point in special relativity is that the relationships between space and time coordinates are intertwined.  Observers moving relative to each other at a constant velocity will experience different perceptions of time and space.  

E=mc2

As already stated a major addition to Lorentz’s theorem by Einstein, is the formulation of Energy = mass x the speed of light in a vacuum square (E=mc2).  This theory states that mass and energy are interchangeable.  Nuclear reactions offer proof of this.  Fair enough.  For example, a small amount of mass may be converted into a large amount of energy. 

Within STR the mainstream narrative offers that this equation is a key element in describing how energy and mass are observed in different inertial reference frames moving relative to each other.  I am not sure this is true.  It can lead to theories about time dilation for example, or as already stated, length contraction where an object that is moving away relative to an observer will appear contracted in the direction of motion (which may be incorrect, more later).  

Much of this is only theory and still open to dispute.  Though E=mc², is a fundamental expression in the theory of relativity, it is not and cannot be used as a direct proof of time dilation or the concept of different clocks running at different speeds.  This would be tautological.  At best it helps describe such phenomena if they exist. 

Implications of STR

The main areas of importance of STR, cited within the mainstream science literature include:

1.     Time-dilation (not as clear cut as presented, scanty proofs, but can be observed),

2.     Red-shift calculations (absolutely nothing to do with STR and eviscerated here),

3.     GPS systems (if STR did not exist these would still work),

4.     Bending of light (this seems correct). 

Two out of four.  The above are not the vital points about STR. There are two implications of STR in my opinion.  More here